Regression sandbox

Sep 16 2017 stats R

library(ggplot2)
library(broom)
library(magrittr)
library(dplyr)
library(knitr)

Logistic regression

One way or another

If we have two binary variables and we want to see if they are associated we could use a logistic regression. How do we decide which variable to be the predictor and which variable to observed variable ?

In theory there shouldn’t be any differences but let’s check with a dummy example:

df = data.frame(x = sample(c(FALSE, TRUE), 100, TRUE))
df$y = df$x
df$y[1:70] = sample(c(FALSE, TRUE), 70, TRUE)

glm(y ~ x, data = df, family = binomial()) %>% tidy %>% 
    kable

term	estimate	std.error	statistic	p.value
(Intercept)	-0.2336149	0.3070802	-0.7607617	0.4467994
xTRUE	1.1745982	0.4256623	2.7594604	0.0057897

glm(x ~ y, data = df, family = binomial()) %>% tidy %>% 
    kable

term	estimate	std.error	statistic	p.value
(Intercept)	-0.4054651	0.3227486	-1.256288	0.2090117
yTRUE	1.1745982	0.4256624	2.759460	0.0057897

df$z = runif(100)
glm(y ~ x + z, data = df, family = binomial()) %>% 
    tidy %>% kable

term	estimate	std.error	statistic	p.value
(Intercept)	-0.5930811	0.5436028	-1.0910191	0.2752645
xTRUE	1.2012521	0.4293265	2.7979921	0.0051421
z	0.6601875	0.8199692	0.8051369	0.4207407

glm(x ~ y + z, data = df, family = binomial()) %>% 
    tidy %>% kable

term	estimate	std.error	statistic	p.value
(Intercept)	-0.1246648	0.5141828	-0.2424523	0.8084297
yTRUE	1.1996170	0.4291206	2.7955243	0.0051816
z	-0.5586854	0.8023449	-0.6963157	0.4862311

Adding another predictor doesn’t change the estimates either.

Interpretation

Just to make sure I understand the estimates correctly. It represents the log odds ratio change for each “unit” of the predictor. In the case of a binary variable, the log odds ratio between the two groups.

glm(y ~ x, data = df, family = binomial()) %>% tidy %>% 
    kable

term	estimate	std.error	statistic	p.value
(Intercept)	-0.2336149	0.3070802	-0.7607617	0.4467994
xTRUE	1.1745982	0.4256623	2.7594604	0.0057897

odds.y.ifx = mean(subset(df, x)$y)/mean(!subset(df, 
    x)$y)
odds.y.ifnotx = mean(subset(df, !x)$y)/mean(!subset(df, 
    !x)$y)
log(odds.y.ifx/odds.y.ifnotx)

## [1] 1.174598

Extreme cases

How efficient is the logistic regression when there is an imbalance between different types of observations ? For example if just a few genomic regions overlap an interesting annotation and I want to test is the overlap is significant.

Let’s look at the worst cases when there are only 1 observation for a particular class.

df = data.frame(y = sample(c(FALSE, TRUE), 100, TRUE))
df$x = 1:nrow(df) %in% sample.int(nrow(df), 1)
glm(y ~ x, data = df, family = binomial()) %>% tidy %>% 
    kable

term	estimate	std.error	statistic	p.value
(Intercept)	0.1010961	0.2012644	0.5023050	0.6154530
xTRUE	15.4649721	1455.3975462	0.0106259	0.9915219

Although the significance is low, the estimate seems quite high. I’ll repeat this process a bunch of time and with different number of supporting observations to have an idea of the distribution.

ext.df = lapply(1:500, function(ii) {
    res = lapply(1:10, function(ssi) {
        df$x = 1:nrow(df) %in% sample.int(nrow(df), 
            ssi)
        glm(y ~ x, data = df, family = binomial()) %>% 
            tidy %>% mutate(rep = ii, ss = ssi)
    })
    do.call(rbind, res)
})
ext.df = do.call(rbind, ext.df)

ext.df %>% filter(term == "xTRUE") %>% ggplot(aes(x = estimate)) + 
    geom_density(fill = "grey50") + facet_grid(ss ~ 
    ., scales = "free") + theme_bw()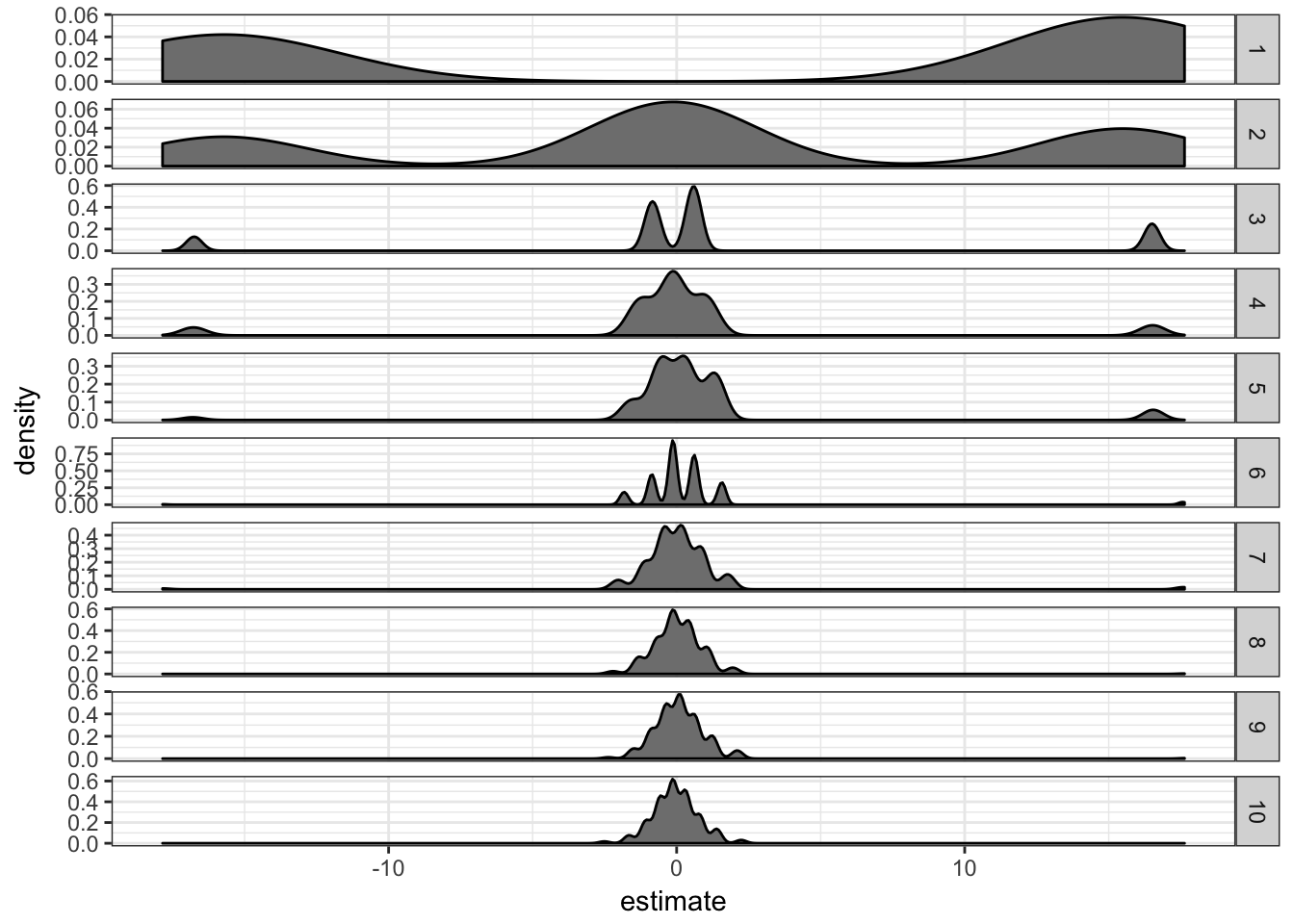

It seems like the estimate “inflation” is problematic mostly when there are only 1 or 2 supporting observations. If there are more than 5 supporting observations the estimate is correctly centered in 0.

This problem is in fact called the problem of separation. There are two approaches to deal with it:

Firth logistic regression.
Exact logistic regression.

The rms package from Frank Harell. It implements a penalized maximum likelihood estimation of the model coefficients through the lrm function which has a penalty= parameter.

library(rms)
extrms.df = lapply(1:200, function(ii) {
    res = lapply(1:10, function(ssi) {
        res = lapply(c(1, 3, 5), function(pen) {
            df$x = 1:nrow(df) %in% sample.int(nrow(df), 
                ssi)
            cc = lrm(y ~ x, data = df, penalty = pen)$coefficient
            data.frame(term = names(cc), estimate = cc, 
                rep = ii, ss = ssi, penalty = pen, 
                stringsAsFactors = FALSE)
        })
        do.call(rbind, res)
    })
    do.call(rbind, res)
})
extrms.df = do.call(rbind, extrms.df)

extrms.df %>% filter(term == "x") %>% ggplot(aes(x = estimate)) + 
    geom_density(fill = "grey50") + facet_grid(ss ~ 
    penalty, scales = "free") + theme_bw()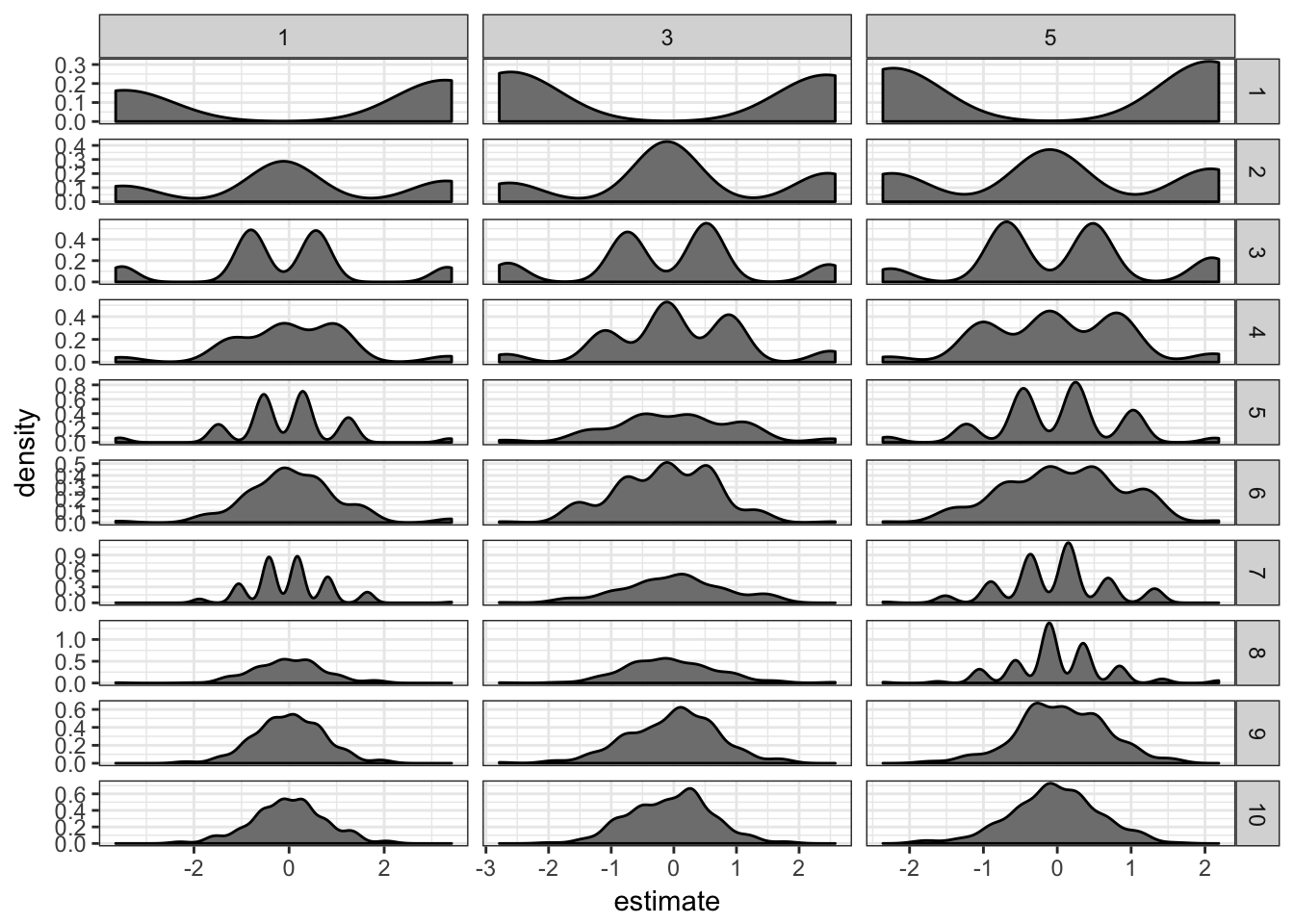

It definitely helps: the estimates are now much closer to 0. I don’t see much difference between penalties 1, 3 or 5.

The logistf package. It implements Firth’s bias reduction method with its logistf function.

library(logistf)
extstf.df = lapply(1:200, function(ii) {
    res = lapply(1:10, function(ssi) {
        df$x = 1:nrow(df) %in% sample.int(nrow(df), 
            ssi)
        cc = logistf(y ~ x, data = df)$coefficient
        data.frame(term = names(cc), estimate = cc, 
            rep = ii, ss = ssi, stringsAsFactors = FALSE)
    })
    do.call(rbind, res)
})
extstf.df = do.call(rbind, extstf.df)

extstf.df %>% filter(term == "xTRUE") %>% ggplot(aes(x = estimate)) + 
    geom_density(fill = "grey50") + facet_grid(ss ~ 
    ., scales = "free") + theme_bw()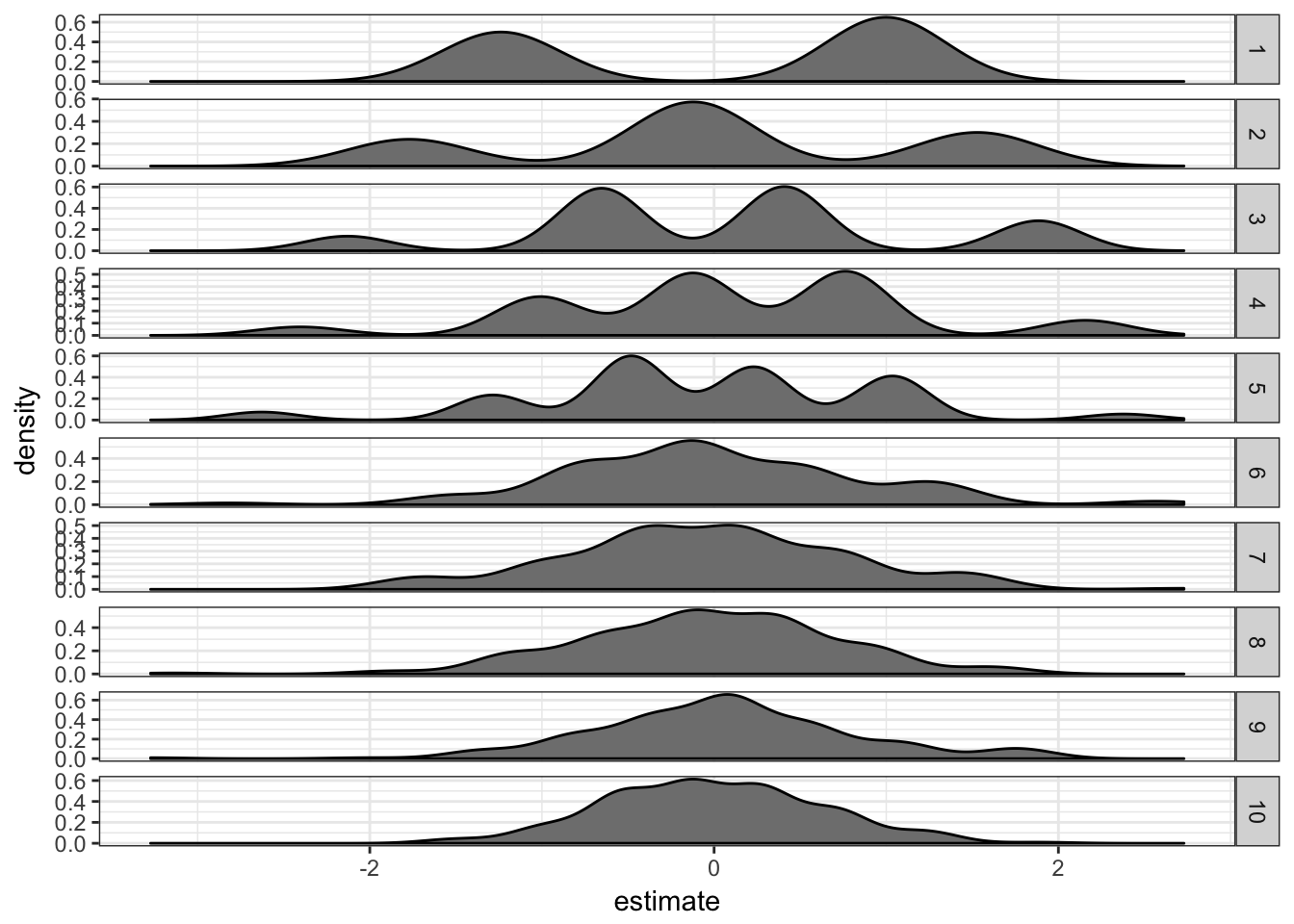

This works well too.

More advanced models

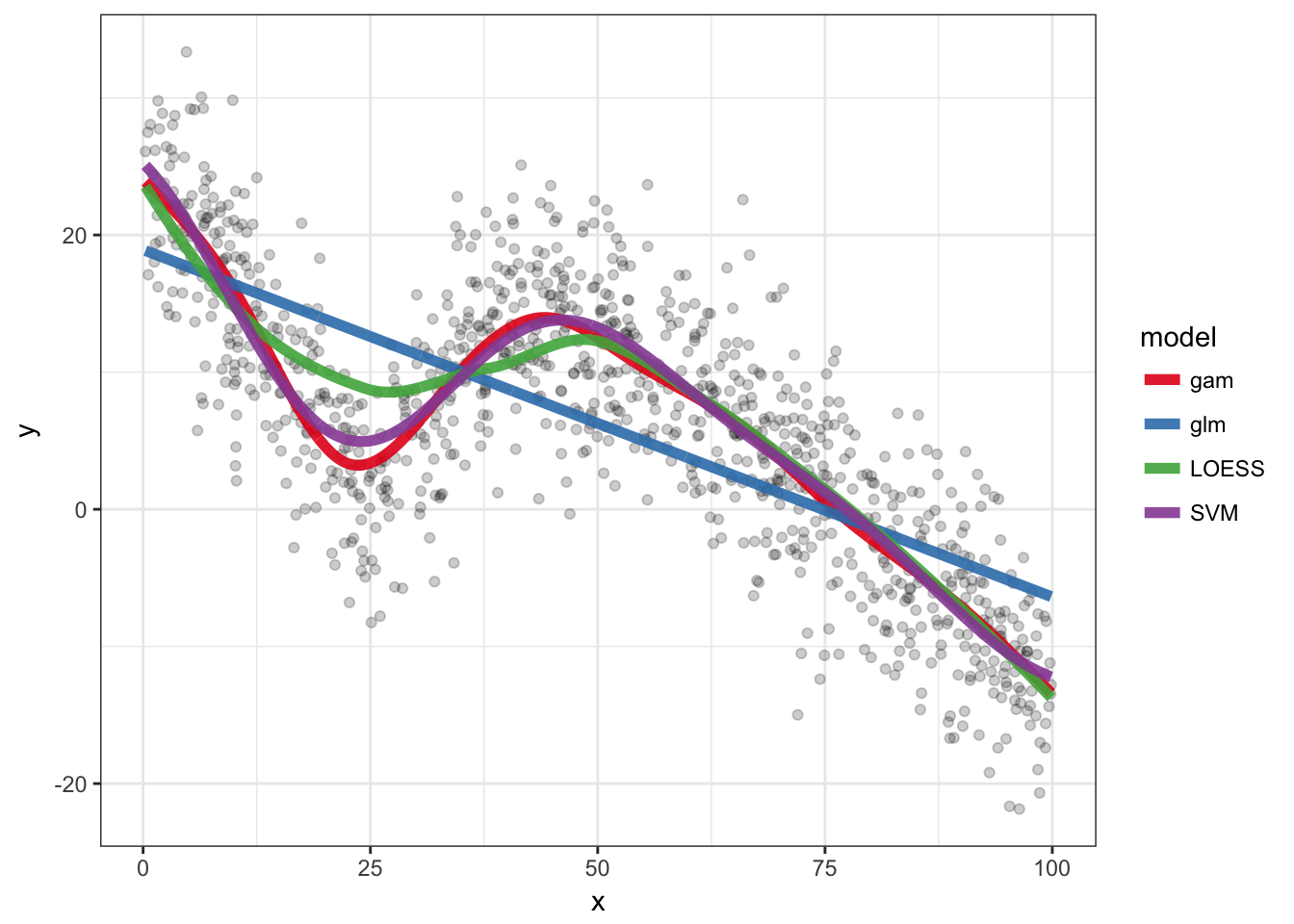
A dummy example with some code for Generalized Additive Models, LOESS and SVM.

nb.samp = 1000
df = data.frame(x = runif(nb.samp, 0, 100))
df$y = rnorm(nb.samp, 0, 5) + abs(df$x - 25)
df$y = ifelse(df$x > 40, rnorm(nb.samp, 0, 5) - df$x * 
    df$x/300 + 20, df$y)
ggplot(df, aes(x = x, y = y)) + geom_point(alpha = 0.5) + 
    theme_bw()